トレードをやっていてそう思ったことはありませんか?
どうせトレードをやるのであれば、手っ取り早くお金を増やしたいですよね?
手っ取り早くお金を増やすならハイレバで高ロットがベストに思えるかもしれませんが、1回で全額失っては話になりません。多すぎず、少なすぎず・・・のロットがベストなのです。
そんな時に役立つのが「ケリーの公式」。
ケリーの公式は不確実性を相手にする賭け事やトレードで使われるもので、複利で運用する場合、資金の何%を賭ければ最大に増やせるかを求めることができる画期的な公式です。
優位性のある手法とケリーの公式さえあれば、世の中の富はあなたの手元に流れ込んできます。
今回はそんな夢のあるケリーの公式をテーマに資金管理について考えます。

数式が出てきますが決して難しいものではりません。
資金管理を考える上で重要になってきますので、ゆっくり考えてみてください。
単利と複利の違いについて
まずは最初に基礎用語として単利と複利について解説します。
単利運用とは常に同じ金額をかけて取引することです。
例えばFXで1ロットでトレードしている場合、いくらお金が増えて減っても、常に同じ1ロットで取引することを単利運用と呼びます。
複利運用とは、取引で増減した資金を考慮して取引量を決める方法です。
例えば、100万円で1ロットで取引していて、資金が増えて110万円になったらロットを上げて1.1ロットで取引するようなやり方です。
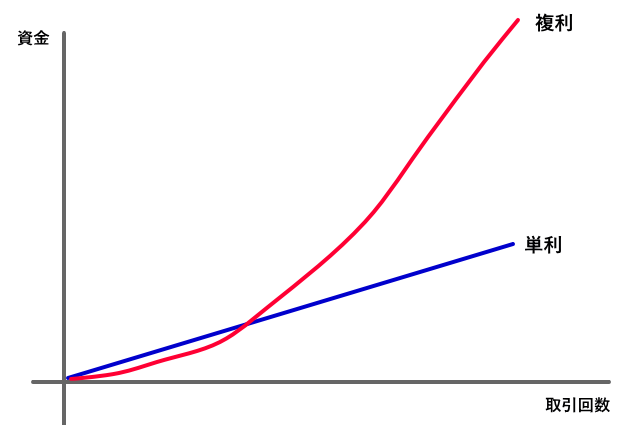
単利と複利では資金の増え方に大きな違いが出ます。
単利運用では口座資金に関わらずトレード毎のロット数が常に同じになるため、資金の増え方はゆっくりです。
その一方で複利運用は口座資金に応じてロット数が大きく変わるので、資金が増えれば増えるほど莫大に資金が増えていきます。
ケリーの公式について
この手法で資金を複利運用するにあたって、資金を最大限に増やすには1回のトレードリスクを口座資金の何%にすればよいか?
という問題があったとします。
一番多く増やしたいんです。
あなたは1回のトレードのリスクをどれくらいにしたら一番多く増やせると思いますか?
毎回資金を100%賭けるとすぐに破産してしまうし、1%くらいだと「最大限に増やす」ことは難しそう・・・。なら何となく30%くらい?
この問題を解くのに使用するのが、ジョン・ケリーという数学者の考案したケリーの公式です。
この公式は以下の通りです。
ただし、
- P=勝率
- R=損益率(勝ちトレードでの平均利益/負けトレードでの平均損失)
この式に従って問題を解いてみましょう。
今回の場合は、勝率60%、損益率1.0ですので
F=0.2ということで、資金の20%を1回のトレードのリスクとすることで資金が最大限に増やせるという結果になります。

お金が一番増えるのなら、それでやるべきでしょ。

ケリーの公式を使ってトレードすると心臓が何個あっても足らないと思うよ。
心臓が剛毛でフサフサで絡みついてるくらいの人じゃないと・・・。
ケリーの公式以上のリスクを取っても意味がない

ケリーの公式から得られる最も重要な情報は、ケリーの公式以上のリスクを取っても、リターンは増えないという点です。
先ほどの例で言えば、ケリーの公式により口座資金の20%をリスクに晒してトレードするのが一番効率よく資金が増えるということになりました。
では、20%以上のリスクだとどうなるのでしょうか?
結論から言うと、20%よりも大きなリスクを取ってトレードしても、20%でトレードした場合よりも資金の伸びは小さくなるのです。
それなら、ケリー以上のリスクを取る意味なんてないですよね?
ですが、損切りをしなかったり、衝動的にナンピンやマーチンをすることで、結果的にケリーを超えてリスクを取っているケースがよく見受けられるのです。

感覚的には分かりにくいですが、これが事実なんです。でも、理屈で知っておくと、無謀な取引が減らせるはずです。
ケリーの公式を使って資金管理するべきか?

ケリーの公式を使って資金管理・ポジションサイジングをしていくと、資金の増え方が最大になりますが、実際にこのやり方で運用していいのでしょうか?
これはノーだと言えます。その理由は3つあります。
1.精神的な問題
ケリーの公式は、信じる度合いを賭ける公式で、この公式を用いる場合はトレード手法の精度が良いほど大きな金額を賭けていくやり方になります。
上の例で出した勝率60%損益率1.0というそれほど大したことのない優位性であっても1回のトレードで20%のリスクを取らなくてはいけません。
1回のトレードで20%のリスクというのは大きすぎです。
口座資金が100万円あったら、1回の取引で20万円をリスクに晒さないといけません。200万円なら40万円です。
トレード毎に資金の20%が上下に変動したら精神的に大きな負担となって、ルールを守る ことも難しくなるでしょう。
資金のボラティリティが激しすぎるのも良いことではないのです。
2.相場の問題
ケリーの公式を使う賭けが、サイコロの出た目で勝敗が決まるようなゲームだったら問題ありませんが、相場の場合は話が変わってきます。
こうなってしまった場合、調子の良かった時の勝率と損益率から求めたリスクで取引しても、実はリスクの取りすぎになってしまうことになります。
なぜなら、相場は変化していくものだからです。
相場が変化すると、それまでの手法の勝率や損益率に変化が生じます。
場合によっては、ずっと勝てていた手法なのに突然使い物にならなくなるケースもあります。
GFFさんはRSIブレイクで2カ月ほどで6億円を稼ぎましたが、突然勝てなくなりました。
詳しくは以下の記事をご覧ください。
3.破産の確率の問題
先ほどの例に出した通り、勝率60%、損益率1.0の手法では20%のトレードリスクで運用していくのが最大に資金が増える計算になりましたが、この条件で破産の確率を求めると、約13%になります。
つまり、複利で資金を最大に増やせるように取引する場合は、ある程度の破産のリスクも覚悟しておかなくてはいけないことになります。
果敢にリスクを取って資金の伸びを最大限にするよりも、破産の確率が0になるまでリスクを下げて取引する方が賢明だと個人的には思っています。

ケリーを選んだら破産する確率が上がる。
両方を取ることなんてできないんですね。
ケリーの公式の使用者
ケリーの公式を実際に使用したトレーダーは数多くいると思いますが、その中でも有名なのはエドワード・オークリーソープです。
彼はケリーの公式を利用してカジノで大きな利益を得ます。
しかし、もうけ過ぎてあらゆるカジノを出来になってしまったため、次は市場に移ってアービトラージを始めます。
アービトラージは現在ではよく知られた手法ですが、当時は画期的で、特に統計を駆使しるスタティスティカル・アービトラージを考案したのはソープと言われています。
そんなアービトラージでもケリーの法則を利用して、ソープは大きな成功を納めます。
しかし、マーケットの魔術師内でソープは「ケリーの公式はリスクを取り過ぎている」と言っています。更にはケリーの半分くらいのリスクでも十分すぎるくらいだと主張しています。
ケリーはあくまでも参考程度にしよう

以上から、ケリーの公式をそのまま使うのは危険だと言えます。
あくまで、最大でどれだけのリスクを取れるのかを把握するためだけに使ったほうがいいと思います。
稀に数ヶ月で資金を何十倍にするトレーダーがいますが、その人たちの多くがその後は大きな損失を被って退場を余儀なくされます。
彼らは多くのリスクを取りすぎたために、調子の良い時は等比級数的に資金を伸ばせる一方で、調子の悪い時は同じスピードで一気に資金を減らしていき、再起不能になるのです。
一気に駆け上って、一気に突き落とされる・・・・。 精神的なダメージは相当なものでしょう。

資金が最も増やせるけど、その分だけリスクが大きくなるって事ね。

だけど、ケリー以上の割合でリスクを取ると、リスクだけが大きくなってリワードが下がるっていう事実もあるんだよ。


そういうこと。ケリーの公式では、求められた値以上のリスクをとっても意味が無いって事も分かるんだ。個人的にはこの点が凄く重要だと思うね。リスクを取るにしてもケリー以下にする。資金管理の原則と言っても良いかも知れない。
ケリーの公式の正しい使い方は、「自分の手法で取れる最大のリスクを知る」この1点だと思います。
「虎穴に入らざれば虎子を得ず」と言いますが、虎穴に無防備のままに入りすぎたら、虎の子供は得られずに、代わりに親虎から食べられる可能性の方が上がるわけです。
「虎穴にどれくらい深くまでなら入って良いか?」
これを数学的に知れるのがケリーの公式と考えたほうが良いでしょう。